FIN 222 Corporate Finance
corporate finance
In Lecture 5 (CH11 and CH12), you were introduced to the concept of systematic risk, as measured by beta. Beta is an indicator of an asset’s exposure (or vulnerability) to systematic risk and evaluates the degree to which an asset’s return is correlated with the market return. Beta is a key parameter in the Capital Asset Pricing Model (CAPM) which is most commonly used asset pricing model for the estimation of required rate of returns on a share (i.e. cost of equity=rE). This assignment consists of two parts. Part I directs you to work with real financial data in Excel and aims to take you through the basic exercise of estimating a company beta and computing statistics which can be evaluated as part of investment decision-making process. Part II requires you to write a report based on interpretations of the outputs obtained from the first part. In this manual, you will also find out how to download historical share price, market index data and interest rates from the web portal.
corporate finance
Details of Questions
PART 1
To successfully complete PART 1, please read each section carefully. You must read “Format and printing requirement” before you produce any outputs. I also encourage you to read the entire manual before you choose your companies for analysis.
If you have read “Format and printing requirement”, then proceed.
- Provide your answers (or outputs) for the following questions.
- All the calculations and computations are required to be produced in Excel (This manual has been designed for you to do this assignment using Microsoft Office Excel 2010).
- Be prepared to use Excel worksheet functions if instructed.
- Apart from what is provided in this manual, any further guidance on the use of Excel functions will not be given. For further help, students should use ‘Help’ function in Excel.
- I would like you to become familiar with notations (or symbols) in [ ] and use those notations to label your answers (and columns) in this part.
1. Download historical prices for two companies and market index into Excel.
Instructions!
- Choose two companies [i] from TWO different industries listed on the Australian Securities Exchange (ASX). To view ASX listed companies, go to http://www.asx.com.au/asx/research/listedCompanies.do
- To download the data, go to http://finance.yahoo.com
- Find a search box titled “Get Quotes” & type the name of your first company [i1]. Then click “Get Quotes”.
- See the menu on the left-hand side. Click “Historical Prices” under “Quotes”.
- See “Set Date Range”. Set Start date as 30th April 2010 and End date as 31th March 2015 (sample period). Click on “Monthly” button. Then Click “Get Prices”.
- 60 month-end price data should now be visible on the screen. Scroll down until you see “Download to Spreadsheet”. Save the data to a file (You will see that date on the spreadsheet is shown as month-start except for 30/04/2010). Don’t worry about them. They are actually month-end data. However, ensure that the company you have chosen has a total of 60 month-end prices and does not exhibit a sudden drastic price fall arising from a share split during the sample period. (If unsure, show your data to your lecturer).
- You will see seven columns in the saved spreadsheet. All we need is Date and Adj. close price [P]. Delete other columns. Currently, the data is in descending order. Go to “Data” tab and click “Sort”. Select “Date” for Sort by and “Oldest to Newest” for order. Click “OK”. The data should now be in ascending order. Save the file again.
- Replicate steps b to g to download data for your second company [i2].
- Replicate steps b to g to download market index data [m]. For this assignment, the market index “All Ordinaries” is to be used. Symbol to be entered to “Get Quotes” box is ^AORD.
- Display the following on the same spreadsheet, i) date, ii) Adj. close price for your first stock [Pi1] , iii) Adj, close price for your second stock [Pi2] and iv) Adj. close price for the market index [Pm]. Then save the file in Excel format. At this point, you should have four columns and 61 rows (The company names do not need to be presented here. Introduce your company names in your report in Part II.)
2. Calculate the monthly realised returns,[Ri1, Ri2, Rm], for your stocks and market index.
Instructions!
- We learnt in Lecture 5 that realised return at t+1 can be calculated as
Rt+l = Divt+l + Pt+l – Pt / Pt - As you are using prices adjusted for dividends, you do not need to consider a dividend component in return calculation if you have chosen a dividend paying stock.
- Three additional columns should be created for your monthly realised returns of i1, i2 and m, which should be available from May 2010. (i.e. a total of 59 monthly returns should be generated.)
- Label your answers correctly.
3. Compute the following for your sample period.
3.1. Monthly average returns [Ri1 Ri2 Rm ]
3.2. Variance [Vari1 Vari2 Varm] of monthly returns
3.3. Standard Deviation [SDi1 SDi2, SDm ] of monthly returns
Instructions!
- To compute the monthly average returns, use Excel function =AVERAGE (data range)
- To compute the variance, use Excel function, =VAR(data range)
- To compute the standard deviation, use Excel function, =STDEV(data range)
- This might help. You are meant to arrive at one value for i1 R and for all the rest.
- Label your answers correctly.
4. Compute the Annual average return [Ri1A Ri2A RmA]. Your yearly interval will start in April and end in March in the following year.
Compute the followings.
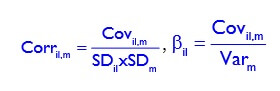
5.1. Covariance [Cov] and Correlation coefficient [Corr] between your first stock’s monthly returns and market returns. Then compute the beta for the 1st stock [ βi1]. Your goal is to arrive at one value for each of the three.
5.2. Covariance [Cov] and Correlation coefficient [Corr] between your second stock’s returns and market returns. Then compute the beta for the 2nd stock [βi2]. Your goal is to arrive at one value for each of the three.
5.3. Covariance [Cov] and Correlation coefficient [Corr] between your 1st stock’s returns and 2nd stock’s returns. Your goal is to arrive at one value for each of the two.

At this point, you should have produced a total of 4 spreadsheets with all your outputs and answers labelled as instructed.
- Spreadsheet 1 should contain outputs for Q1-Q4.
- Spreadsheet 2 should contain outputs for Q5.1.
- Spreadsheet 3 should contain outputs for Q5.2.
- Spreadsheet 4 should contain outputs for Q5.3.
6. Additionally, compute the beta by regressing stock returns on market returns.
6.1. Compute [βi1] using a regression analysis.
6.2. Compute [βi2] using a regression analysis.
Instructions!
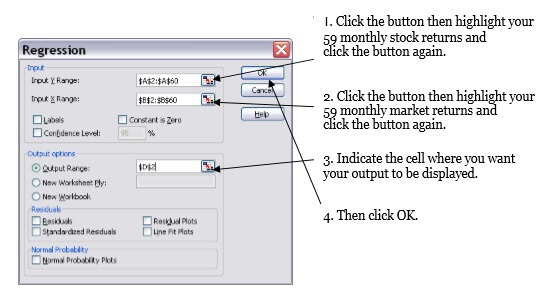
A beta can also be computed using a regression analysis. To do this, you will only need to work with 59 monthly stock returns and 59 monthly market returns.
To answer 6.1,
- Open a new worksheet in the current file, copy and paste date, your monthly stock returns and monthly market returns [Ri1, Rm] as in step a in the previous question. Then go to “Data” tab “Data analysis” on the far right “Regression” then click “OK”
(If you don’t see ‘Data analysis’ under ‘Data’ tab then click ‘Options’ under ‘File’ tab. Go to ‘add-ins’ from the left-hand side menu. On the bottom, you will see a drop-down menu next to ‘Manage’. Select ‘Excel Add-ins’ then Click ‘Go’ and tick ‘analysis toolpak’ and click ‘OK’. ‘Data analysis’ should now appear under ‘Data’ tab.) - You will see the following pop-up monitor. Proceed as follows

- Summary output will be displayed. Under ANOVA, the coefficient on X variable represents a beta of your stock i1[Note: See Figure 12.7 on Page 374 of our text book. The coefficient on X variable (=beta) represents the slope of this line]. This beta estimate obtained from regression analysis should be identical to the beta from Question 5.1.
- To answer 6.2, replicate steps a to b. (Make sure you replace il with i2 wherever relevant.)
- Summary output will be displayed. Under ANOVA, the coefficient on X variable represents a beta of your stock i2. This beta estimate obtained from regression analysis should be identical to the beta from Question 5.2.
7. Estimate the required rate of return for your stocks [E(Ri1), E(Ri2)] as at 31st March 2015 using the CAPM. Use 6.5% as a market risk premium and the 10year Australian Government bond rate as at 31st March 2015 as a risk-free rate [rf].
7.1. Establish the CAPM equation and compute the required rate of return for the first stock [E(Ri1)] on the 5th spreadsheet in which you produced [βi1] using a regression analysis. You must present the CAPM with corresponding values used.
7.2. Compute the required rate return for the second stock [E(Ri2)] on the 6th spreadsheet in which you produced [βi2] using a regression analysis. You must present the CAPM with corresponding values used.
Instructions!
a. 10-year Government bond rates can be obtained from http://www.rba.gov.au/statistics/tables/index.html#interest-rates. See “Capital market yields – Government bonds-Daily” under Interest Rates.
- Spreadsheet 5 should contain outputs for Q6.1 and Q7.1.
- Spreadsheet 6 should contain outputs for Q6.2 and Q7.2.
At this point, you should have produced a total of 6 spreadsheets with all your outputs and answers labelled properly.
PART II
1. Which stock would be more sensitive to a change in economic condition? Please answer by referring to and interpreting the value of an appropriate measurement obtained in Part I.
2. How closely do your first and second stocks move together? Please answer by referring to and interpreting the value of an appropriate measurement obtained in Part I.
3. Based on your results in Part I, is each of your stocks underpriced or overpriced? And why? Consequently, which recommendation would you make for each stock, “Buy/Hold” or “Sell/don’t buy”?
4. Suppose that you invested 40% of your wealth in your first stock and 60% in the market index (i.e. All ordinaries) to form a two-asset portfolio.
4.1. How would you measure the total risk of your portfolio? Please compute. Clearly show and label all the data you import from Part I. No workings, no marks.
4.2. What is a 95% prediction interval for your portfolio’s 2015 April return?
4.3. By forming the above two-asset portfolio, were you able to achieve diversification benefit? Please answer by referring to and interpreting the value of an appropriate measurement obtained in Part I.
5. Suppose that you invested 20% of your wealth in your first stock, 50% in your second stock, 20% in the market index, and 10% in the 10-year Australian Government bond to form a four-asset portfolio.
5.1. Compute the beta of your portfolio.
5.2. Compute the required rate of return of your portfolio as at 31st March 2015.
5.3. You wish to reduce your portfolio’s exposure to a change in market condition. What can you do?
6. “Two stocks that have the same correlation coefficients with the market will have the same betas.” Is this statement true or false? Please support your answer using the following formulae.
Format/Printing /Submission Requirements
Format Requirements
PART I
corporate finance
1. Generate all your outputs in 6 separate spreadsheets as follows.
- Spreadsheet 1 should contain outputs for Q1-Q4.
- Spreadsheet 2 should contain outputs for Q5.1.
- Spreadsheet 3 should contain outputs for Q5.2.
- Spreadsheet 4 should contain outputs for Q5.3.
- Spreadsheet 5 should contain outputs for Q6.1 and Q7.1.
- Spreadsheet 6 should contain outputs for Q6.2 and Q7.2.
2. Font for both numerals and words should be Arial size 8.
3. i) covariance and ii) betas should show full decimal places. For others, keep 4 decimal points.
4. In answering Q5, you must use the method instructed in this manual.
5. Label your final outputs using notations suggested. The example follows.
| 3.3SDi1 SDi2,SDm | 0.XXXX | 0.XXXX | 0.XXXX |
| 3.3 Vari1 Vari2, Varm | 0.XXXX | 0.XXXX | 0.XXXX |
6. I do not mind you drawing symbols(notations) by hand.
7. The use of appendix is not allowed.
PART II
- Your written report can be typed in any preferred font style.
- The report should be typed in size 12 with no spacing or margin requirement.
- When answers are discussed, question numbers (i.e. 1,2,3…) are to be clearly presented.
- Use your own words. Reference wherever necessary.
- Use a Harvard system of referencing.
- Reference (or bibliography) should be provided at the back of your report.
- The use of appendix is not allowed.
- Your written report must not exceed 5 pages (excluding reference).
Printing Requirements
1. For Spreadsheets 1-4, print out each spreadsheet twice.
- Starting with Spreadsheet 1, make one printout as usual showing all your numerical answers.
- Create a copy of Spreadsheet 1. Make a second printout which must show row and column headings and your cell formulas used to generate your calculation. First, to make formulas visible, on a copy of Spreadsheet 1, go to “Formulas” tab -> Click “Show Formulas” within “Formula Auditing” section. Second, to show row and column headings, go to “Page Layout” tab -> within “Sheet Options” section -> under “Headings” -> tick “Print” box.
In the second printout, the above sample output should appear as below.A B C D 62 3.3 SDil, SDi2, SDm =STDEV(B3: D61) =STDEV(C3: C61) =STDEV(D3: D61) 63 3.3 Varil, Vari2, Varm =VAR(B3: D61) =VAR(C3: C61) =VAR(D3: D61) - c. Repeat a and b for Spreadsheets 2-4.
2. For Spreadsheets 5 and 6, print out each spreadsheet once.
- Make one printout as usual showing all your numerical answers.
- A separate spreadsheet with formula view is NOT required as you were required to present the used formula on the numerical spreadsheet.
3. Before you print, make sure your cell size is appropriate (so that it does not take up too much space). To see how to change column width and row height, see http://office.microsoft.com/en-us/excel-help/change-the-column-width-and-row-heightHP001216383.aspx#BMmouse. To fit your spreadsheet into one page, you will need to reduce margins. Go to “File” tab “Print”. The “Print Preview” is shown on the right of the window. Activating the first button at bottom right-hand corner will allow you to reduce margins for both left/right and top/bottom. (DO NOT USE “FIT SHEET ON ONE PAGE” BUILT-IN FUNCTION UNDER SCALING. IT’S GOING TO MAKE YOUR FONT EXTREMELY SMALL and DIFFICULT TO BE READ.)
4. The spreadsheet with numbers is to be followed by the spreadsheet with corresponding formula view. For example, spreadsheet 1 should be followed by the spreadsheet with formula view then spreadsheet 2 followed by the spreadsheet with formula view and so forth.
5. Your written report will then follow this set of spreadsheet
corporate finance
The Best Assignment help is one of the best website for assignment help. For more details you may contact us at thebestassignmenthelp@gmail.com
corporate finance
visit at :BEO2431 Risk Management Models